MATRICES LABORATORIO 3
//LAB-3
#include<iostream>
#include<math.h>
using namespace std;
double x;
const int n=2,m=2;
int F,m1,i,j,suma,M;
int matriz[n][m],a[n][m],b[n][m];
int leermatriz();
int sumaelementos();
int impresion();
int identidad();
int central();
int leomatriza();
int leomatrizb();
int sumamatrices();
int promedio();
int promas();
int trans();
int main ()
{//1)DECLARACION
int opcion;
do
{
cout<<"*********MENU DE MATRICES**********\n\n";
cout<<"1)LECTURA UNA MATRIZ \n";
cout<<"2)IMPRESION O ESCRITURA DE LA MATRIZ \n";
cout<<"3) MATRIZ IDENTIDAD \n";
cout<<"4)ELEMENTOS CENTRALES\n";
cout<<"5)LECTURA DE MATRIZ A\n";
cout<<"6)LECTURA DE MATRIZ B\n";
cout<<"7)SUMA DE MATRICES\n";
cout<<"8)SUMANDO MATRICES\n";
cout<<"9)PROMEDIO DE LA MATRIZ\n";
cout<<"10)ELEMENTOS SOBRE EL PROMEDIO\n";
cout<<"MATRIZ TRANSPUESTA\n";
cout<<" DIGITE <0> PARA SALIR \n\n";
cout<<"*************\n\n";
cout<<" ELIJA UNA OPCION : "; cin>>opcion;
//2)ASIGNACION
switch (opcion)
{
case 1:
{
cout<<"leer elementos de una matriz\n";
leermatriz();//invocacion
} //FIN DEL CASO 1
break;
case 2:
{
cout<<"impresion o escritura de una matriz\n";
cout<<"los elementos son\n";
impresion();
} //FIN DEL CASO 2
break;
case 3:
{
cout<<"matriz identidad\n";
identidad();
//FIN DEL CASO 3
}
break;
case 4:
{
cout<<"elementos centrales\n";
central();
}
break;
case 5:
{
cout<<"lectura de la matriz A[i][j]\n";
leomatriza();
}
break;
case 6:
{
cout<<"lectura de la matriz B[i][j]\n";
leomatrizb();
}
break;
case 7:
{
cout<<"suma de matrices A y B \n";
sumamatrices();
}
break;
case 8:
{
cout<<"suma de elementos\n";
sumaelementos();
}break;
case 9:
{
cout<<"promedio de la matriz\n";
promedio();
}break;
case 10:
{
cout<<"elementos sobre el promedio\n";
promas();
}break;
case 11:
{
cout<<"matriz transpuesta";
trans();
}break;
}
}// FIN DE SWITCH }
#include<iostream>
#include<math.h>
using namespace std;
double x;
const int n=2,m=2;
int F,m1,i,j,suma,M;
int matriz[n][m],a[n][m],b[n][m];
int leermatriz();
int sumaelementos();
int impresion();
int identidad();
int central();
int leomatriza();
int leomatrizb();
int sumamatrices();
int promedio();
int promas();
int trans();
int main ()
{//1)DECLARACION
int opcion;
do
{
cout<<"*********MENU DE MATRICES**********\n\n";
cout<<"1)LECTURA UNA MATRIZ \n";
cout<<"2)IMPRESION O ESCRITURA DE LA MATRIZ \n";
cout<<"3) MATRIZ IDENTIDAD \n";
cout<<"4)ELEMENTOS CENTRALES\n";
cout<<"5)LECTURA DE MATRIZ A\n";
cout<<"6)LECTURA DE MATRIZ B\n";
cout<<"7)SUMA DE MATRICES\n";
cout<<"8)SUMANDO MATRICES\n";
cout<<"9)PROMEDIO DE LA MATRIZ\n";
cout<<"10)ELEMENTOS SOBRE EL PROMEDIO\n";
cout<<"MATRIZ TRANSPUESTA\n";
cout<<" DIGITE <0> PARA SALIR \n\n";
cout<<"*************\n\n";
cout<<" ELIJA UNA OPCION : "; cin>>opcion;
//2)ASIGNACION
switch (opcion)
{
case 1:
{
cout<<"leer elementos de una matriz\n";
leermatriz();//invocacion
} //FIN DEL CASO 1
break;
case 2:
{
cout<<"impresion o escritura de una matriz\n";
cout<<"los elementos son\n";
impresion();
} //FIN DEL CASO 2
break;
case 3:
{
cout<<"matriz identidad\n";
identidad();
//FIN DEL CASO 3
}
break;
case 4:
{
cout<<"elementos centrales\n";
central();
}
break;
case 5:
{
cout<<"lectura de la matriz A[i][j]\n";
leomatriza();
}
break;
case 6:
{
cout<<"lectura de la matriz B[i][j]\n";
leomatrizb();
}
break;
case 7:
{
cout<<"suma de matrices A y B \n";
sumamatrices();
}
break;
case 8:
{
cout<<"suma de elementos\n";
sumaelementos();
}break;
case 9:
{
cout<<"promedio de la matriz\n";
promedio();
}break;
case 10:
{
cout<<"elementos sobre el promedio\n";
promas();
}break;
case 11:
{
cout<<"matriz transpuesta";
trans();
}break;
}
}// FIN DE SWITCH }
while (opcion !=0);
cout<<endl;cout<<"\n";
system("pause");
return 0;
}//FIN DEL PROGRAMA
int leermatriz()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"M["<<i<<"] M["<<j<<"]:";
cin>>matriz[i][j];
}
}
int sumaelementos()
{
suma=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
suma=suma+matriz[i][j];
}
cout<<"la suma de los elementos es ="<<suma<<endl;
}
int impresion()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int identidad()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int central()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
if (i==j)
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int leomatriza()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"A["<<i<<"] A["<<j<<"]:";
cin>>a[i][j];
}
}
int leomatrizb()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"B["<<i<<"] B["<<j<<"]:";
cin>>b[i][j];
}
}
int sumamatrices()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
matriz[i][j]= a[i][j]+b[i][j];
}
}
int promedio()
{
suma=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
suma=suma+matriz[i][j];
}
x=suma/(n*m);
cout<<"el promedio es ="<<x<<endl;
}
int promas()
{
M=0;
m1=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
if(matriz[i][j]>x)
M=M+1;
if(matriz[i][j]<x)
m1=m1+1;
}
cout<<"los mayores son "<<M<<"los menores son"<<m<<endl;
}
int trans()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
matriz[i][j]=matriz[j][i] ;
}
}
cout<<endl;cout<<"\n";
system("pause");
return 0;
}//FIN DEL PROGRAMA
int leermatriz()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"M["<<i<<"] M["<<j<<"]:";
cin>>matriz[i][j];
}
}
int sumaelementos()
{
suma=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
suma=suma+matriz[i][j];
}
cout<<"la suma de los elementos es ="<<suma<<endl;
}
int impresion()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int identidad()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int central()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
if (i==j)
cout<<"M["<<i<<"] M["<<j<<"]:"<<matriz[i][j]<<endl;
}
}
int leomatriza()
{
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"A["<<i<<"] A["<<j<<"]:";
cin>>a[i][j];
}
}
int leomatrizb()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
cout<<"ingrese los elementos \n";
cout<<"B["<<i<<"] B["<<j<<"]:";
cin>>b[i][j];
}
}
int sumamatrices()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
matriz[i][j]= a[i][j]+b[i][j];
}
}
int promedio()
{
suma=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
suma=suma+matriz[i][j];
}
x=suma/(n*m);
cout<<"el promedio es ="<<x<<endl;
}
int promas()
{
M=0;
m1=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
if(matriz[i][j]>x)
M=M+1;
if(matriz[i][j]<x)
m1=m1+1;
}
cout<<"los mayores son "<<M<<"los menores son"<<m<<endl;
}
int trans()
{
for (i=1;i<=n;i++)
for (j=1;j<=m;j++)
{
matriz[i][j]=matriz[j][i] ;
}
}








 :
:


![[T]_{xyz} = \begin{bmatrix}
\sigma & \tau_{y} & \tau_{z} \\
\tau_{y} & 0 & 0 \\
\tau_{z} & 0 & 0
\end{bmatrix}](https://upload.wikimedia.org/math/6/7/2/6726ffdd0c1a05e10f3256802762d2b8.png)


 son las tensiones sobre la sección transversal: tensión normal o perpendicular, y las tensiones tangenciales de torsión y cortante.
son las tensiones sobre la sección transversal: tensión normal o perpendicular, y las tensiones tangenciales de torsión y cortante. , son los esfuerzos internos: esfuerzo axial, momentos flectores y bimomento asociado a la torsión.
, son los esfuerzos internos: esfuerzo axial, momentos flectores y bimomento asociado a la torsión.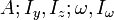 , son propiedades de la sección transversal de la viga: área,
, son propiedades de la sección transversal de la viga: área,  ) y tercera (
) y tercera ( )
) 


