EVAP2

ELECTRICIDAD

La electricidad (del griego ήλεκτρον élektron, cuyo significado es ‘ámbar’) es el conjunto de fenómenos físicos relacionados con la presencia y flujo de cargas eléctricas. Se manifiesta en una gran variedad de fenómenos como los rayos, la electricidad estática, la inducción electromagnética o el flujo de corriente eléctrica. La electricidad es una forma de energía tan versátil que tiene un sinnúmero de aplicaciones, por ejemplo: transporte, climatización, iluminación y computación.

La electricidad se usa para generar:

• luz mediante lámparas
• calor, aprovechando el efecto Joule
• movimiento, mediante motores que transforman la energía eléctrica en energía mecánica
• señales mediante sistemas electrónicos, compuestos de circuitos eléctricos que incluyen componentes activos (tubos de vacío, transistores, diodos y circuitos integrados) y componentes pasivos como resistores, inductores y condensadores.

FASORES:

Es una cantidad compleja que se emplea para representar funciones del tiempo que varían de forma senoidal.   es un número complejo con:

1. módulo: la amplitud de la magnitud que representa.
2. fase: la fase de dicha magnitud en t=0.

El fasor se relaciona con las funciones senoidales a través de la siguiente expresión:

Para poder usarlo en las ecuaciones integro-diferenciales se necesita ver cómo responden a esas operaciones.

Diferenciación con fasores

Si tenemos una función g(t) con su parte real x(t) y su parte imaginaria y(t), y definimos la función:

                                    

Al final:

Las relaciones que tenemos en la diferenciación son:

Integración con fasores

Con la función h(t) definida como la integración de f(t):

Las relaciones que hay en la integración se pueden ver a continuación:

Por lo tanto, se pueden resolver las ecuaciones integro-diferenciales que aparecen en régimen permanente senoidal mediante la utilización de fasores. Esto se debe a que las derivadas y las integrales se transforman en multiplicaciones y divisiones por y así estas ecuaciones se convierten en algebraicas mediante fasores.

Representación fasorial

Forma polar

Los fasores suelen indicarse matemáticamente también en forma polar, es decir como un módulo y un ángulo. Por ejemplo la expresión:

V = 311 sen (2π 50 t + ¼ π)

Se puede representar como un fasor de la siguiente manera:

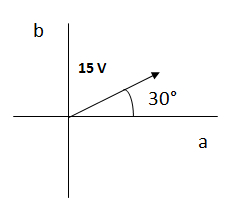V = 311 V

ω = 2π 50 (para una f = 50 Hz)

Φ = 45 ° (o ¼ π)

En forma polar se escribe como 311 (45°) V.

Forma binómica

Otra forma de expresar a un fasor o número complejo, es la forma binómica, es decir como: a + j b siendo a la parte real y b la parte imaginaria.

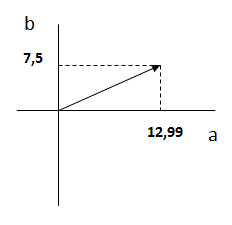Con las relaciones trigonométricas seno, coseno y tangente, podemos calcular las componentes de la forma binómica (a y b) a partir del módulo del fasor y de su ángulo (forma polar) o bien hallar el módulo del fasor y su ángulo a partir de la forma binómica.

Forma binómica a polar

Si tenemos el fasor dado en forma binómica y queremos conocer el módulo, lo calculamos como la hipotenusa del triángulo. El ángulo se calcula como el arco tangente del cateto opuesto sobre el adyacente.

Forma polar a forma binómica

Forma binómica = a + j b

Suma y resta de fasores

Para sumar o restar dos fasores es conveniente tenerlos en forma binómica, por lo tanto se hace la suma o resta componente a componente.

Multiplicacion y división de fasores

Es más simple hacerlas en forma polar. Se multiplican o dividen los módulos según corresponde y se suman los argumentos (para el caso de la multiplicación) o se los resta (para el caso de la división).

1.- DIAGRAMA DE FLUJO

1-Declaración

R , C , F , Pi , Z , Xc , A

2- Asignación

R = 8w

C= 30uf

A = 30°

Pi = 3.1416

Xc = 1000000 / 2 x Pi x F x C

3- Proceso:

a) Z = R - jXc

b) Tan(A) = Xc / R

4- Resultados

a) Z = R - jXc

    Z = 8- j(1000000 / 188.48 x F)

b) Tan30° = (1000000 / 188.48 x F) / 8

              F = 1.150 Hz

Programacion de cociente de fasores en DevC++

#include <iostream>

using namespace std;

int main()

{

// (1)Declaracion

int vmax1,vmax2;

long double Vfasor1/Vfasor2;

constant cos30=0.15,cos51=0.7,sen20=0.9,sen15=0.6,j;

//(2)Asignacion

cout<<"ponga el primer voltaje:";cin>>vmax1;

cout<<"ponga el segundo voltaje:";cin>>vmax2;

cout<<"V1/V2=Vm1/Vm2*[cos(a-b)+jsen(a-b)];\n\n";

//(3)Proceso

Vfasor1/Vfasor2=vmax1/vmax2*[cos_30°(cos_51-sen_15j)+sen_20*(cos_51j+sen15)];

//Resultado

cout<<"El cociente por la forma fasorial es:";

cout<<Vfasor/Vfasor2;

return 0;

}